Reflexiones Geométricas

Hay reflexiones en todas partes... en espejos, cristales, y en este lago.  ... ¿ves lo que pasa?
¡Los puntos están a la misma distancia de la línea central!
... y ...
La reflexión tiene el mismo tamaño que la imagen original
La línea central se llama línea de reflexión ...
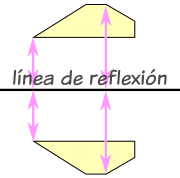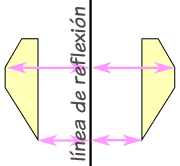
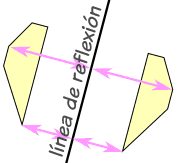
... y no importa en qué dirección vaya el reflejo, la imagen reflejada siempre tiene el mismo tamaño, pero en la otra dirección:
Una reflexión es un volteo con respecto a una línea

¿Cómo lo puedo hacer yo solo?

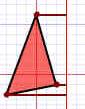
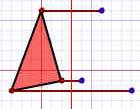
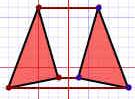
	Hazlo paso a paso. A cada esquina de la figura:
	1. Mide desde el punto de la línea de reflexión (con una línea que llegue en ángulo recto)	2. Mide la misma distancia en el otro lado y marca un punto allí.	3. ¡Conecta todos los puntos nuevos!

Nombres

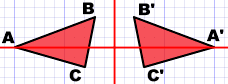
Lo normal es nombrar cada esquina con una letra, y usar una pequeña raya (llamadaprima) para marcar las esquinas reflejadas. Aquí, el original es ABC y la imagen reflejada es A'B'C'

Algunos trucos

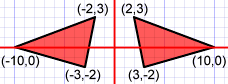
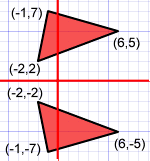
Eje X Si la línea de reflexión es el eje X, sólo cambia (x,y) por (x,-y)

Eje Y Si la línea de reflexión es el eje Y, cambia (x,y) por (-x,y)

Doblando papel Si esto te falla, ¡sólo tienes que doblar la hoja de papel por la línea de reflexión y mirar a través del papel!